Tracé en boucle

Oublions pour un temps notre problème et voyons comment nous pourrions tracer « point par point » sur $[-3\ensuremath{\: ; \,}3]$ la courbe représentative d'une fonction $g$ vérifiant :

$$\frac{g(b)-g(a)}{b-a}=2$$

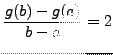
pour tous réels distincts $a$ et $b$ de $[-3\ensuremath{\: ; \,}3]$ et $f(-3)=-1$ .

On peut par exemple subdiviser le segment $[-3\ensuremath{\: ; \,}3]$ en segments de longueurs 0,25 et réfléchir au moyen d'obtenir les images par $f$ de chacune des extrémités des segments de la subdivision.

Il suffit de penser que $\frac{g(x+0,25)-g(x)}{x+0,25-x}=2$ , c'est-à-dire $g(x+0,25)=......+g(x)$ .

On peut donc calculer $g(x+0,25)$ si l'on connaît $g(x)$ .

On va donc partir du point de coordonnées $(-3\ensuremath{\: ; \,}-1)$ et obtenir de proche en proche les coordonnées de plusieurs points de la courbes en faisant des petits sauts de 0,25 et en s'arrêtant à 3 :

S:=NULL; // on crée une suite de points  vide au départ
X:=-3;  // au départ X vaut -3
Y:=-1;  // au départ Y vaut -1
tantque X<=3  faire  // tant que s'écrit tantque en XCAS
   S:=S,point(X,Y);  // on  rajoute le point de coordonnées (X,Y) à notre liste
   X:=X+0.25; // on avance de 0,25 à chaque tour de boucle
   Y:=0.5+Y; // on sait que g(X+0,25)=0,5+g(X) 
ftantque:;  // f comme fin de la boucle
polygone_ouvert(S); // on relie les points de la liste S à la règle

et on découvre sans surprise qu'il s'agit d'un segment de droite.