XCAS et la géomérie dynamique au lycée

Un argument souvent soulevé par ses détracteurs est que XCAS fonctionne principalement en ligne de commande. Notre expérience avec les élèves nous incite à dire qu'il ne s'agit pas d'un inconvénient mais plutôt d'un avantage pour eux : les élèves de nos classes sont en effet habitués à dialoguer via leur ordinateur sur les sites de messagerie instantanée. Le petit bémol qu'on pourrait apporter est qu'avec XCAS, il ne faut pas faire de fautes d'orthographe !

Les commandes sont de plus en français et adaptées aux besoins des élèves français car créées par des professeurs de l'Institut Joseph FOURIER de l'Universite Joseph FOURIER de Grenoble et testées grâce à l'IREM de Grenoble. Que dites-vous de :

parallele, droite, segment, aire, longueur, angle, resoudre, graphe, cercle, circonscrit, simplifier, factoriser, fonction_derivee,symetrie, projection,...?

Le mode de construction d'une figure et de résolution du problème correspond de même à la démarche suivie par l'élève sur sa feuille de papier.

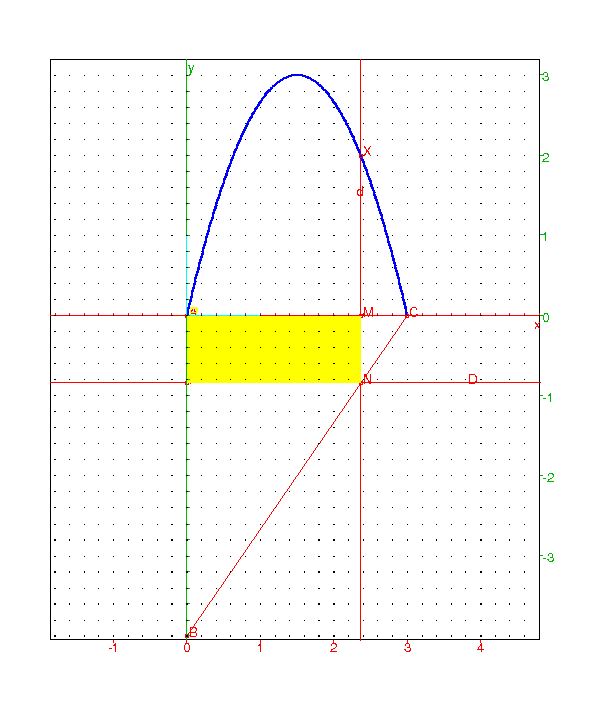
Pour illustrer notre propos, considérons par exemple le problème classique suivant donné en classe de Seconde :

ÉNONCÉ :

On considère un triangle ABC rectangle en A tel que AC=3 et AB=4. Soit M un point quelconque du segment [AC]. On construit le rectangle AMNP tel que N appartienne à [BC] et P à [AB].
Étudiez l'aire du rectangle AMNP en fonction de la position de M.

Commençons par ouvrir une fenêtre de géométrie en tapant simultanément sur Alt et g puis définissons les points A et B dans un repère judicieusement choisi. On utilise point(x,y) ( ou même point(z) pour les terminales ) :

A:=point(0,0)   //  plaçons A
B:=point(0,-4)  // plaçons B tel que AB=4 en laissant le 1er quadrant libre pour y tracer la courbe à la fin de la séance

Définissons ensuite le point C tel que le triangle ABC soit direct, rectangle en A et que l'on ait $AC=\frac{3}{4}AB$ à l'aide de la commande triangle_rectangle :

triangle_rectangle(A,B,3/4,C)

Créons maintenant un réel quelconque de [0;3] que l'on puisse faire varier à la souris à l'aide de la commande assume(t=[valeur de départ,mini,maxi]) :

assume(t=[1,0,3])

Définissons maintenant le point M d'abscisse variable t :

M:=point(t,0)

Pour définir N, commençons par définir la perpendiculaire en M à la droite (AC). La syntaxe est tout à fait naturelle grâce à perpendiculaire(Point,Droite). C'est bien ce que l'élève doit tracer sur sa feuille de papier pour tracer le rectangle :

d:=perpendiculaire(M,droite(A,C))

Définissons ensuite N comme l'intersection de d et (BC) grâce à inter_unique :

N:=inter_unique(d,droite(B,C))

Pour obtenir P, nous commençons par définir la parallèle à (AC) passant par N à l'aide de parallele(Point,Droite) :

D:=parallele(N,droite(A,C));

puis l'intersection de D et $(AB)$  :

P:=inter_unique(D,droite(A,B))

Il ne reste plus qu'à définir le rectangle APNM grâce à la commande polygone :

R:=polygone(A,P,N,M)

et à dessiner le rectangle dépendant du paramètre t :

couleur(R,jaune+rempli)

En faisant varier t à la souris, le rectangle bouge .

Définissons maintenant l'expression de l'aire du rectangle dépendant de t. Appelons-la par exemple Surf :

Surf:=aire(R)

Donnons son expression simplifiée :

simplifier(Surf)

qui répond :

$-\dfrac{4}{3} t^{2}+4t$

Définissons le point X de la courbe représentative de la fonction associée d'abscisse t :

X:=point(t,Surf)

Traçons enfin la courbe représentative de la fonction associée à l'aide de la commande graphe :

graphe(Surf,t=0..3,couleur=bleu)

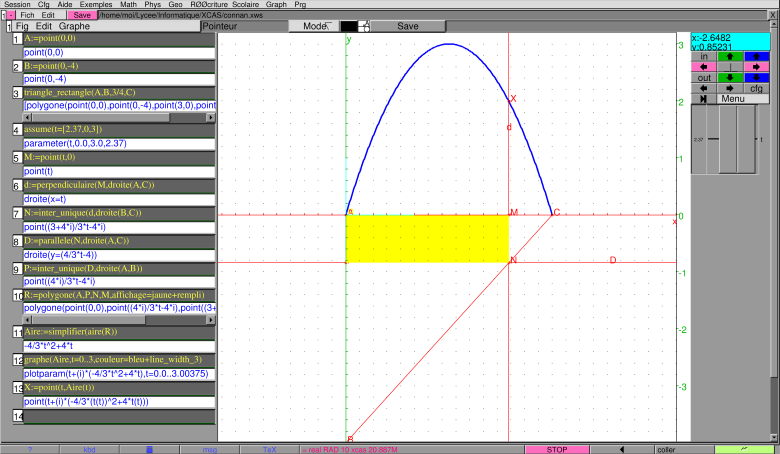
Voici une visualisation statique :