XCAS et les suites

Il existe principalement deux types de sujets proposés pour l'épreuve expérimentale du Bac S : les problèmes que peuvent traiter les logiciels de géométrie dynamique que nous venons d'étudier et l'étude de suites à l'aide du deuxième pilier de l'Éducation Nationale, le tableur.

Nous allons donc nous intéresser à ce deuxième type de sujet. Voici par exemple le sujet 5 de la banque d'exercices de 2007 :

Étude de la suite $u_{n+1}=a\cdot u_n+b$ pour a et b donnés : convergence et valeur de la limite.

On supposera par la suite que $a\neq 1$ . En effet, dans le cas contraire, $u_{n+1}=u_n+b$  : la suite est donc arithmétique et ne mérite pas une étude poussée...

On construit une procédure donnant $u_n$ en fonction de a, b et le premier terme $u_0$ . On traite le cas n=0 pour initialiser. Ensuite il suffit de rentrer l'expression de $u_n$ en fonction du terme précédent :

u(n,a,b,uo):={
si n==0 alors return uo;
sinon a*u(n-1,a,b,uo)+b; // C'est-à-dire u(n)=a*u(n-1)+b
fsi
}:;

Par exemple, pour a=0,7, b=1 et $u_0=1$ , en tapant :

u(100,.7,1,1);u(500,.7,1,1) // le 100-ème et le 500-ème terme

on obtient :

3.333333333,3.333333333

Et pour a=-1/2, b=1 et $u_0=1$ , en tapant :

u(100,-0.5,1,1);u(500,-0.5,1,1)

on obtient :

0.6666666667,0.6666666667

REMARQUE : on peut préférer fixer a,b et uo hors de la procédure et définir u de manière plus standard ainsi :

u(n):={
si n==0 alors return uo;
   sinon a*u(n-1)+b;
fsi    
}:;

et alors :

a:=0.7
b:=1
uo:=1
u(100);

On a l'impression d'avoir de sérieux candidats pour la valeur de la limite. Pour confirmer cette intuition, représentons graphiquement les premiers termes de la suite. On crée une séquence S de coordonnées, vide au départ, et à laquelle on ajoute les points coordonnées $(k,u_k)$ pour k variant de 0 à n :

AffSuite(n,a,b,uo):={
local S,k;
S:=NULL;  // S est vide au départ : il n'y a pas encore de points
affichage(point_carre+rouge); // pour l'esthétique...
pour k de 0 jusque n pas 1 faire
   S:=S,point(k,u(k,a,b,uo)); // on rajoute le point de coordonnées $(k,u_k)$ à notre liste
fpour
}

On affiche les valeurs de la suite ainsi que la limite présumée issue de notre calcul :

 AffSuite(20,-.5,1,1),graphe(0.66666667,x=0..20,couleur=bleu)

et on obtient pour a=0,7, b=1 et $u_0=1$  :

et pour a=-1/2, b=1 et $u_0=1$  :

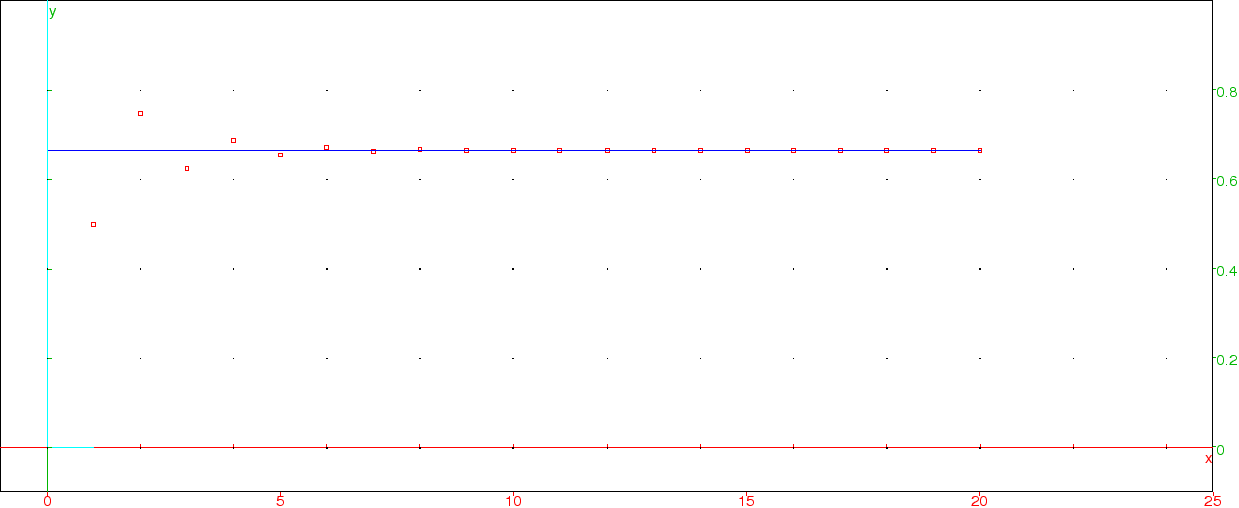
Notre intuition est confortée.

REMARQUE : cette manière de procéder peut sembler naturelle et proche d'une démarche « papier-crayon », mais n'est pas optimale informatiquement. On peut, pour la culture des élèves, évoquer le problème crucial de la complexité d'un algorithme.

En effet, dans AffSuite, on recalcule u(k,a,b,uo) à chaque tour de boucle : pour aller jusqu'au rang n, on effectue donc $1+2+3+\cdots+n=\frac{n(n+1)}{2}$ calculs.

On dit que la complexité de l'algorithme est de l'ordre de $n^2$ .

Voici une manière plus « informatique » et efficace de procéder :

AffSuiteBis(n,a,b,u0):={
local S,k,uk;
affichage(point_carre+rouge);
S:=point(0,u0);  // premier terme
k:=u0;
pour k de 1 jusque n pas 1 faire
  uk:=a*uk+b;
  S:=S,point(k,uk); // on rajoute le point de coordonnées (k,u_k) à notre liste
fpour
}

On effectue n calculs pour avoir AffSuiteBis(n,a,b,uo) : la complexité est maintenant de l'ordre de n.

Le problème de la complexité est ici accessoire car dans les deux cas l'ordinateur effectue ces calculs simples très rapidement. Cependant, quand les algorithmes sont plus sophistiqués, cela peut permettre de sauver beaucoup de temps. On peut même évoquer le système RSA qui assure la sécurité des transactions sur internet ou bancaire et dont la sécurité est basée sur la complexité informatique du cassage du code théoriquement possible mais hors du temps humain pour l'instant.

Revenons à présent à notre problème.

Nous pouvons aussi remarquer que $u_{n+1}=f(u_n)$ , avec f(x)=ax+b.

Nous pouvons représenter la suite directement avec la fonction XCAS plotseq((f(x),u(0),n) :

plotseq(0.7*x+1,1,10)

qui affiche un graphe que les élèves de terminales savent interpréter :

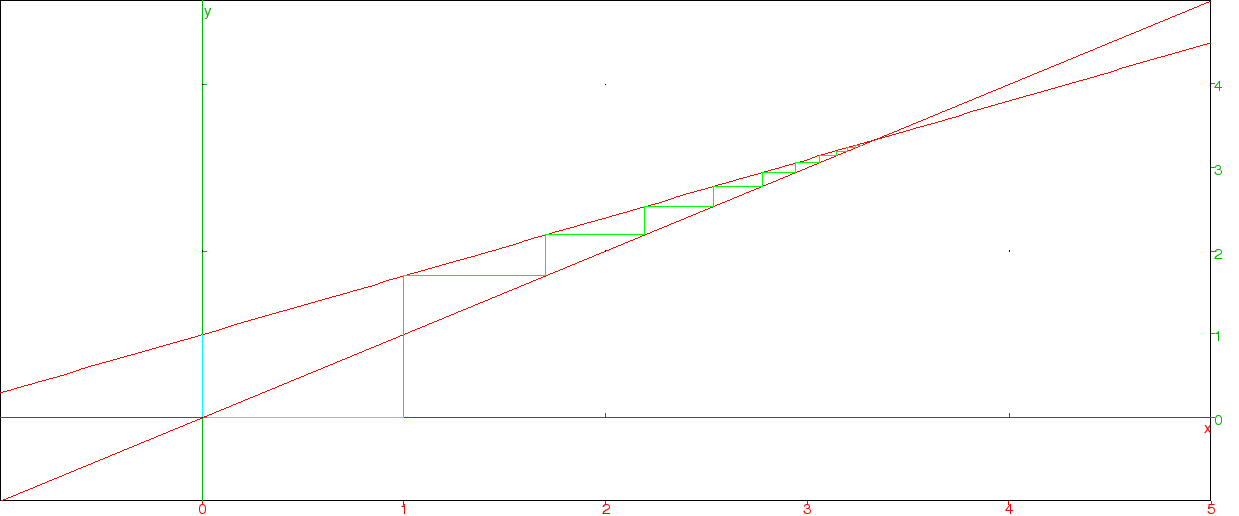
Le candidat pour la limite semble être l'intersection des droites d'équations y=ax+b et y=x. On obtient la solution avec resoudre(équation,inconnue) :

resoudre((7/10)*x+1=x,x)

On obtient :

$\dfrac{10}{3}$

Il ne reste plus qu'à le démontrer...

Soit p la solution de ax+b=x. Elle existe bien car on a supposé $a\neq 1$ .

Alors, en effectuant la différence membre à membre de $u_{n+1}=au_n+b$ et $p=ap+b$ , on obtient :

$$u_{n+1}-p=a(u_n-p)$$

Donc la suite $(u_n-p)$ est géométrique de raison a et de premier terme $u_0-p$ .

On obtient donc

$$u_n=(u_0-p)a^n+p$$

Vérifions :

expu(n,a,b,uo):={
local p,c;
p:=resoudre(a*x+b=x)[0]; // la solution de l'équation
c:=simplifier(uo-p);  // on simplifie l'écriture de u0-p
return(c*a^n+p)  // on renvoie (uo-p)*a^n+p
}:;

Par exemple, toujours avec a=0,7, b=1 et $u_0=1$  :

expu(n,7/10,1,1)

On obtient : $\dfrac{-7\cdot \left(\dfrac{7}{10}\right)^{n}}{3}+\dfrac{10}{3}$

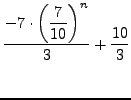
Comparons maintenant les graphes :

AffSuite(20,7/10,1,1),graphe(expu(x,7/10,1,1),x=0..20,couleur=bleu)

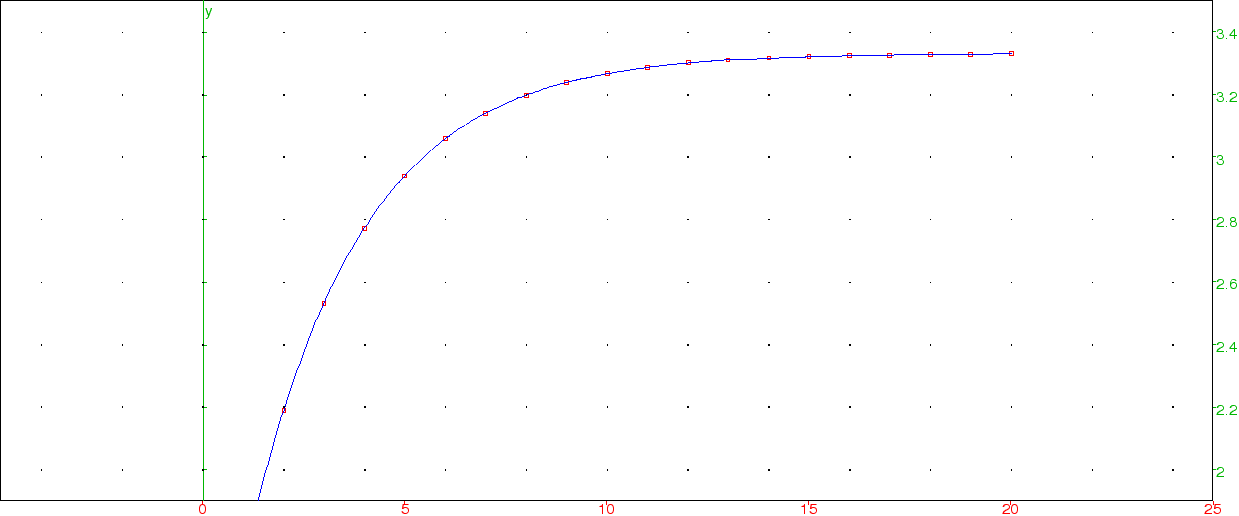
Et voilà...Nous pouvons même nous payer le luxe de vérifier que expu vérifie la formule de récurrence initiale dans le cas général, c'est-à-dire pour a, b, $u_0$ quelconques !

Ce confort n'est bien sûr possible qu'avec un logiciel de calcul formel...

expu(n+1,a,b,uo)-(a*expu(n,a,b,uo)+b)

donne : $(a\cdot uo+b-uo)\cdot \dfrac{1}{a-1}\cdot (a)^{n+1}-\left(\dfrac{b}{a-1}\right... ...uo+b-uo)\cdot \dfrac{1}{a-1}\cdot (a)^{n}-\left(\dfrac{b}{a-1}\right))\right)-b$

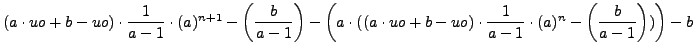
Oups...

simplifier(ans()) // simplifie le résultat précédent

qui renvoie bien 0.

C'est mieux ! Nous pouvons aller jusqu'à calculer la limite de la suite dans le cas général :

limite(expu(n,a,b,uo),n,+infinity)

Mais XCAS ne sait que répondre...il faut bien sûr distinguer les cas :

assume(a>0) and assume(a<1); // 0<a<1
limite(expu(n,a,b,uo),n,+infinity)

donne :

$\dfrac{-b}{a-1}$

et dans le cas a>1 :

assume(a>1);
limite(expu(n,a,b,uo),n,+infinity)

on obtient : infinity

Ainsi, XCAS nous permet non seulement d'observer le résultat mais surtout de le démontrer grâce à ses facultés de calcul formel. Nous allons illustrer plus précisément ce point dans le paragraphe suivant.