Preuve d'un théorème

Les coniques ne sont plus au programme de terminale mais sont encore sources d'activités. Nous allons ici nous occuper d'un théorème concernant le tracé de la tangente à une conique et le prouver à l'aide de XCAS ce qui n'est possible qu'avec un logiciel de calcul formel.

Le théorème initial est le suivant :

Construction de la tangente à une conique

Soit $\Gamma$ une conique de foyer F et de directrice associée D. La tangente à $\Gamma$ en tout point M qui n'appartient pas à l'axe focal coupe D en un point T tel que l'on ait $\overrightarrow{FM}\cdot\overrightarrow{FT}=0$

Nous allons adapter l'énoncé au cas d'une demi-ellipse définie à l'aide d'une fonction :

ÉNONCÉ

Soient a et b deux réels strictement positifs tels que a>b et f la fonction définie sur [-a,a] par

$$f(x)=b\sqrt{1-\dfrac{x^2}{a^2}}$$

Notons $\Gamma$ la courbe représentative de f dans un repère orthonormé.
Soit F le point de coordonnées $(\sqrt{a^2-b^2}\ensuremath{\: ; }0)$ et D la droite d'équation $x=\frac{a^2}{\sqrt{a^2-b^2}}$ .
Montrez que la tangente à $\Gamma$ en tout point M d'ordonnée non nulle coupe D en un point T tel que l'on ait $\overrightarrow{FM}\cdot\overrightarrow{FT}=0$

Nous pouvons bien sûr commencer par illustrer des cas particuliers en prenant un point mobile sur $\Gamma$ et en observant que la propriété reste vérifiée.

Nous allons sauter cette étape, notre propos étant de montrer comment un logiciel de calcul formel permet non seulement d'illustrer mais aussi de prouver un théorème général.

Nous commençons par définir la fonction f :

f:=x->b*sqrt(1-(x^2/a^2)):;

Nous allons ensuite considérer un point quelconque de $\Gamma$ d'absisse t, avec $t\in]-a,a[$  :

assume(a>0):;
assume(t>-a) and assume(t<a):;
M:=point(t,f(t)):;

Pour définir la tangente d à $\Gamma$ en M, nous allons introduire la fonction dérivée de f que nous noterons fp. Nous utiliserons les commandes XCAS abscisse et ordonnee qui renvoient l'abscisse et l'ordonnée d'un point bien sûr, et la commande droite qui permet de définir une droite de multiples façons ( par une équation, deux points, comme intersection de deux plans, une représentation paramétrique,... ). Nous la définirons ici par l'équation classique $y=f'(x_M)\times(x-x_M)+f(x_M)$  :

fp:=fonction_derivee(f):;
d:=droite(y=fp(abscisse(M))*(x-abscisse(M))+ordonnee(M)):;

Mode « muet »

Vous noterez que chaque ligne de commande se termine par :; ce qui indique à XCAS qu'il doit évaluer cette ligne mais sans renvoyer de résultat. En effet, aucun tracé ne peut être effectué pour l'instant car aucune valeur numérique n'est affectée aux paramètres a, b et t.

Il reste à définir le point F et la droite D :

F:=point(sqrt(a^2-b^2),0):;
D:=droite(x=a^2/sqrt(a^2-b^2)):;

Le point T est l'intersection des droites d et D.

On utilise la commande inter_unique(ensemble1,ensemble2) :

T:=inter_unique(d,D):;

Il ne reste plus qu'à calculer le produit scalaire $\overrightarrow{FM}\cdot\overrightarrow{FT}$ à l'aide de scalar_product.

scalar_product(vecteur(M,F),vecteur(T,F))

Calcul vectoriel

Un vecteur pour XCAS est une liste de coordonnées entre deux crochets tout comme l'est un point. L'opération $M-F$ est donc licite pour XCAS. Pour ne pas semer le trouble dans les esprits des élèves du lycée, on peut remplacer M-F par coordonnees(M)-coordonnees(F), ou bien, pour éviter de calculer avec des systèmes de coordonnées, on peut préférer travailler sur les affixes en rentrant

scalar_product(affixe(M)-affixe(F),affixe(T)-affixe(F))

On peut également demander à Bernard PARISSE de créer une commande vecteur(M1,M2) synonyme de M2-M1 pour l'ordinateur mais moins choquante pour les élèves. C'est ce que j'ai fait...et obtenu une heure plus tard ! Encore un point fort de XCAS...

Ainsi :

scalar_product(vecteur(F,M),vecteur(F,T))

qui donne :

$\left(t-\sqrt{a^{2}-b^{2}}\right)\left(\dfrac{(-a^{4}+a^{2}t^{2})\sqrt{a^{2}-b^{2}}}{-a^{4}+a^{2}t^{2}+(a^{2}-t^{2}) b^{2}}-\sqrt{a^{2}-(b^{2})}\right)+$

$\qquad\qquad\dfrac{b\sqrt{1-\dfrac{t^{2}}{a^{2}}}\left(a\sqrt{a^{2}-t^{2}}\cdo... ...rt{a^{2}-b^{2}}\right)}{-a^{4}+a^{2}t^{2}+\left(a^{2}-t^{2}\right)\cdot b^{2}}$

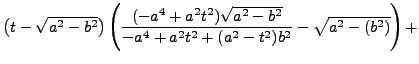
Ouh la la...Voici un calcul qui a de quoi déprimer n'importe quel élève de lycée. Heureusement, nous pouvons faire faire « le sale boulot » à XCAS grâce à la commande simplifier et se concentrer sur le problème géométrique sans être gêné par les difficultés de calcul algébrique.

Cette fois-ci :

simplifier(scalar_product(vecteur(M,F),vecteur(T,F))

renvoie bien 0, ce qui prouve notre théorème car les calculs ont été effectués dans le cas général.