Quelques exercices de MAO (maths assistées par ordinateur)

Exercice 1 Noyau, image

Qu'est-ce que l'endomorphisme de $\mathbb{R}^2$ d'expression analytique canonique

$$\bsyc x'&=&-\displaystyle\frac {1}{5}x-\displaystyle\frac {2}{5}y\\ y'&=&\displaystyle\frac {3}{5}x+\displaystyle\frac {6}{5}y \esyc$$

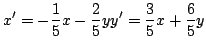
Vous aurez besoin de déterminer la matrice A associée, le noyau de A grâce à nullspace(A) qui en renvoie une base, l'image avec basis(A). Ensuite, à vous d'essayer des petits calculs sur A pour deviner sa nature.

Exercice 2 Puissances de matrices

1. Soit $$A=\frac{1}{3}\begin{pmatrix} 0&-2&-2\\ 2&0&-1\\ 2&1&0 \end{pmatrix}$$.
   1. Calculer $A^2,A^3$ et $A^4$.
   2. Montrer que $\{A,A^2,A^3,A^4\}$ est un groupe pour le produit matriciel de $\mathcal{M}_3(\mathbb{R})$.

2. Pour chacune des matrices $A$ suivantes, calculer $A^n$ pour tout $n\in\mathbb{N}$.
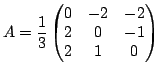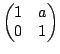   1. $\begin{pmatrix}1&a\ 0&1\end{pmatrix}$ avec $a\in\mathbb{R}$.
   2. La matrice $J_p$ de $\mathcal{M}_p(\mathbb{R})$ dont tous les coefficients sont égaux à 1.

Exercice 3 Inverse d'une matrice

Soit 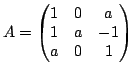$A=\begin{pmatrix}1&0&a\ 1&a&-1\ a&0&1 \end{pmatrix}$. Pour quelles valeurs de $a$, la matrice $A$ est-elle inversible. Calculez alors l'invesre de $A$.

Exercice 4 EDO

Testez MuPAD sur les équations suivantes

1. $(x+1)y'-xy=0$
2. $(1+x^2)y'+xy=3x^3+3x\qquad (1+x^2)y'+xy=1$
3. $xy'+2y=x/(1+x^2)$
4. $y'=\vert y\vert$
5. $\sqrt{1-x^2}y'-y^2-1=0$
6. $y''-3y'+2y=xe^x+\sin(x)$
7. $x^2y''+3xy'+y=0$

Exercice 5 Division euclidienne de polynômes

1. On voudrait conjecturer à l'aide de MuPAD le reste de la division euclidienne de $A$ par $B$ sachant que $A=\pa{(\sin t)X+\cos t}^n$ par $B=X-1$.

   Déterminez ce reste pour des valeurs particulières de $n$. Conjecture ? Prouvez votre conjecture...

   Reprenez le même exercice avec $B=X^2+1$. Pour vous aider dans votre conjecture, vous pourrez utiliser la fonction combine(expr,sincos) qui permet de linéariser une expression trigonométrique et la fonction coeff(p,x,n) qui permet d'isoler le coefficient du polynôme p en $x^n$.

2. Montrez que $A=X+3X^2+5X^3+5X^4+3X^5+X^6$ divise $B=(X+1)^{6n+1}-X^{6n+1}-1$. Vous pourrez utilisez au choix la fonction solve(equation,inconnue) ou factor(polynome) pour trouver les racines de $A$.

Exercice 6 Avec sommation

Trouvez la valeur de $$\sum_{n=1}^{+\infty}\displaystyle\frac {1}{1^2+2^2+\cdots+n^2}$$

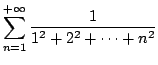
Exercice 7 Trigo

Résolvez l'équation $\arccos(x)=\arcsin(2x)$

Exercice 8 Études de fonctions

1. Étudiez la fonction $x\mapsto x\arctan(x)$ en portant une attention particulière au comportement asymptotique.

2. Étudiez $x\mapsto \sqrt[5]{(x^2-1)^2(x+11/3)}$.

Exercice 9 Ipp

On pose $I_n=\int_0^{\pi/2}\sin^nt$d$t$. Exprimez $I_{n+2}$ en fonction de $I_n$.

Exercice 10 Système

Résoudre $\bsyc x+ay+z+t&=&1\ x+y+az+t&=&b\ x+y+z+at&=&1 \esyc$

Exercice 11 Mini-chaînes de Markov...