Aidons la mafia

Les chaînes de Markov sont issues de la théorie des probabilités et utilisent des outils d'algèbre linéaire qui nous intéressent aujourd'hui. Elles permettent de simuler des phénomènes aléatoires qui évoluent au cours du temps. Nous allons les découvrir à travers l'étude d'un exemple simple.

Zlot, Brzxxz et Morzgniouf sont trois villes situées respectivement en Syldavie, Bordurie et Bouzoukstan. Des traficants de photos dédicacées du groupe ABBA prennent leur marchandise le matin dans n'importe laquelle de ces villes pour l'apporter le soir dans n'importe quelle autre. On notera pour simplifier $V_1$, $V_2$ et $V_3$ ces villes et $p_{ij}$ la probabilité qu'une marchandise prise le matin dans la ville $V_i$ soit rendue le soir dans la ville $V_j$. La matrice $(p_{ij})_{1\leqslant i \leqslant 3\ 1\leqslant j\leqslant 3}$ est appelée matrice de transition de la chaîne de Markov. Que s'attend-on à observer sur les colonnes d'une matrice de transition ?

Supposons que $P$ soit connue et vaille

$$P=\begin{pmatrix}0,8 &0,3 &0,2\ 0,1&0,2&0,6\ 0,1&0,5&0,2\end{pmatrix}$$

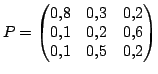
Les traficants se promenant de ville en ville, il peut être utile de visualiser leurs déplacements par le diagramme de transition suivant

On notera $x_i^{(k)}$ la proportion de traficants qui se trouvent au matin du jour $k$ dans la ville $V_i$. En probabilités, on appelle vecteur d'état tout élément $(x_1,\cdots,x_n)$ de $\mathbb{R}^{+n}$ tel que $x_1+\cdots+x_n=1$.

Ainsi, $x^{(k)}=\pa{ x_1^{(k)},x_2^{(k)},x_3^{(k)}}$ est un vecteur d'état.

On montre que les vecteurs d'état de la chaîne sont liés par la relation

$$x^{(k)}=P\cdot x^{(k-1)}$$

et donc

$$x^{(k)}=P^k\cdot x^{(0)}$$

Supposons que le chef de la mafia locale dispose de 1000 traficants qui partent tous le matin du jour 0 de la ville de Zlot. Quelle sera la proportion de traficants dans chacune des villes au bout d'une semaine ? d'un mois ? d'un an ?

Le parrain voudrait que la proportion moyenne de traficants soit stable d'un jour sur l'autre. Il recherche donc les vecteurs d'état $x$ vérifiant l'équation $P\cdot x=x$. Vous apprendrez après l'été à résoudre de manière systématique ce genre de problème. Nous allons pour l'heure nous débrouiller sans appui théorique mais avec Maple et la fonction linsolve(A,B) qui permet de résoudre les équations du type AX=B avec A une matrice, B un vecteur connu et X le vecteur inconnu. Comment procéder ?